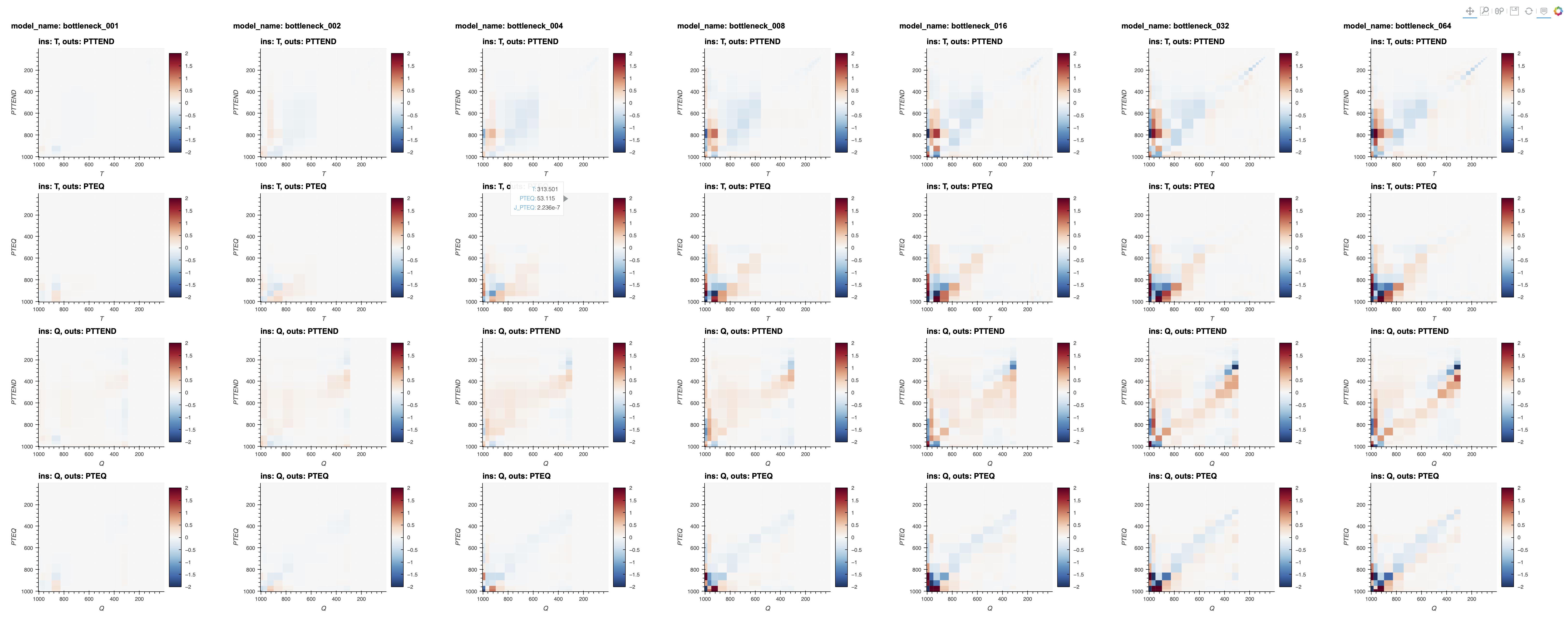
Linearization of NN Surrogate Model

We compute linearization of the NN surrigate f(x) = y, to understand sensitivity to different inputs.

Linearization of $f(x) = Ax + b$, can be computed by taking the gradiant $grad~f(x)$ around $x$. Since f(x) is vector valued we compute a jacobian instead: $A = J_x(f(x))$.

Jacobian of Temperature and Humidity Tendencies

• We can compare empirical Jacobian of surrogate NN with reference CRM computations.
• While the general structure is present in the surrogate, it still somewhat noisy.
• We plan to add Jacobian structure as an additional regularization during optimization to (hopefully) encourage stability during intergration into the climate model.

  To compute the Jacobian, we sample 10000 data inputs from desired region, compute a jacobian around each sample using NN autodifferentiation and then average. We found that this computation is more stable then computing Jacobian around a mean input.

Comparison to Reference CRM

Click on figure for interactive visualization

Jacobian CAM4 FCN NN	Reference from CRM (Fig 8. Kuang 2012)

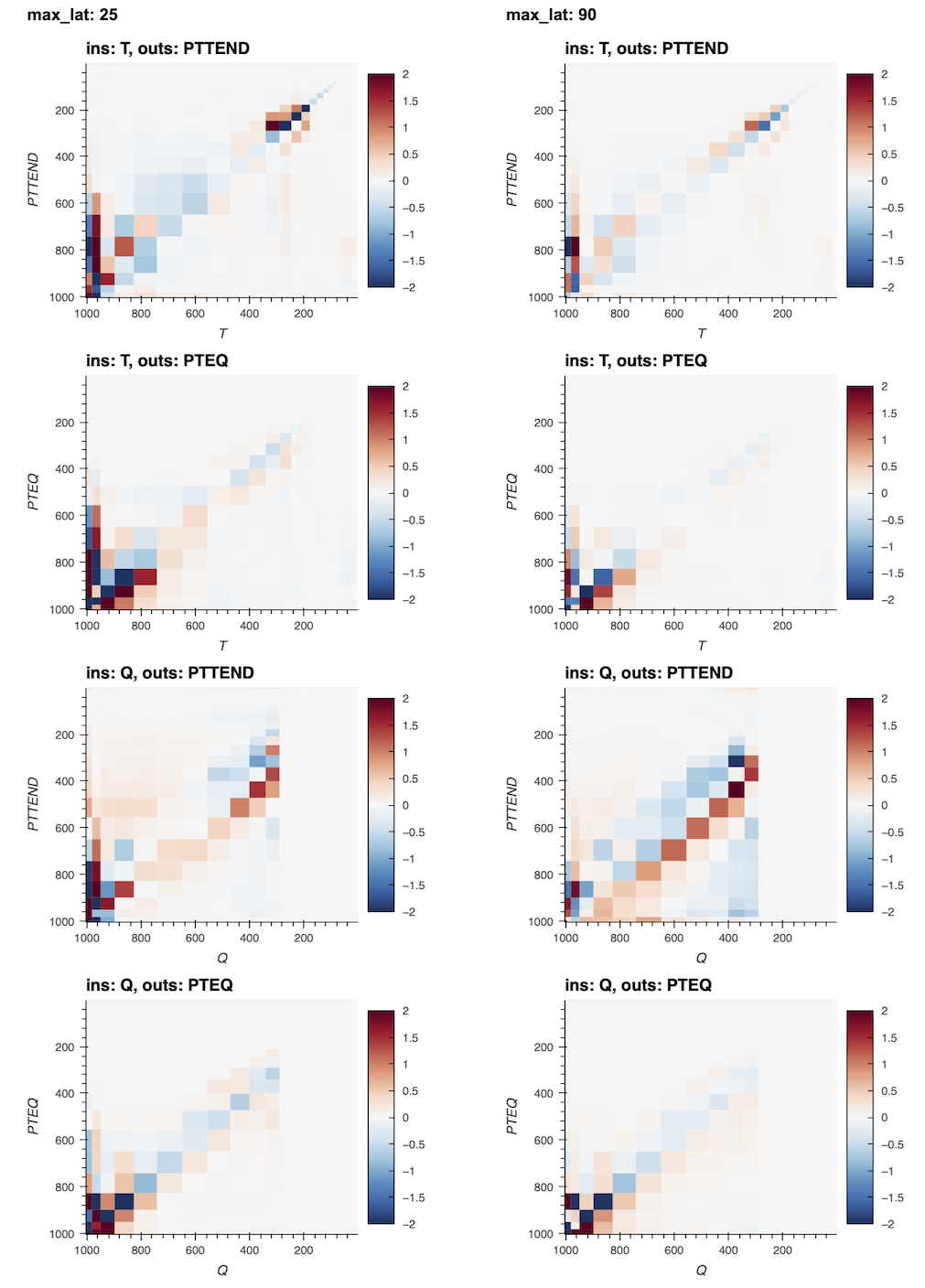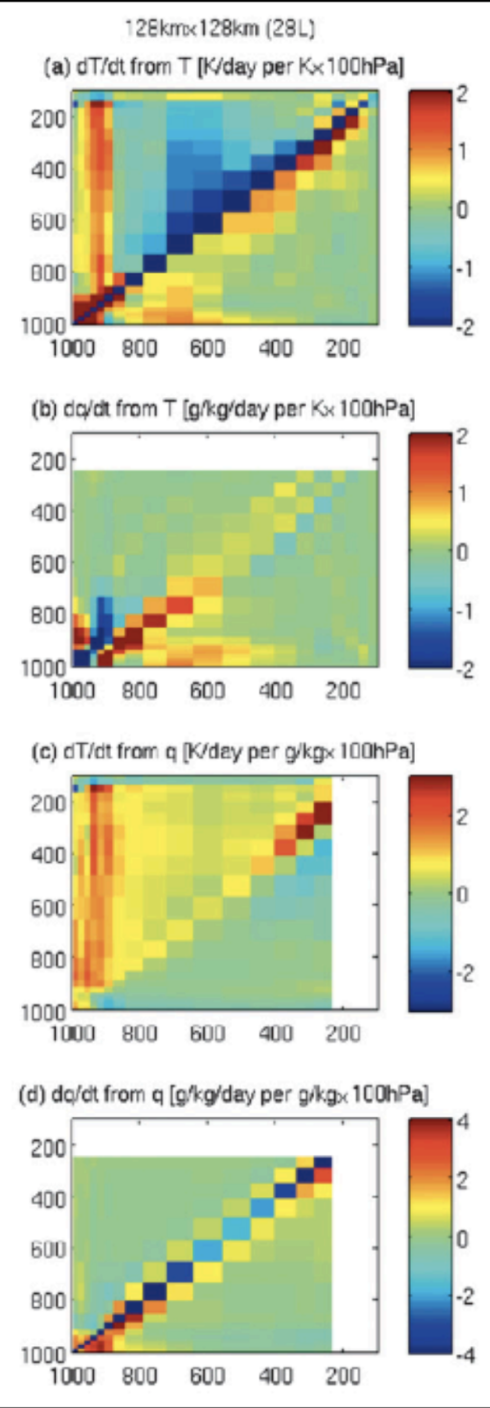Jacobian SPCAM FCN NN	Reference from CRM (Fig 8. Kuang 2012)

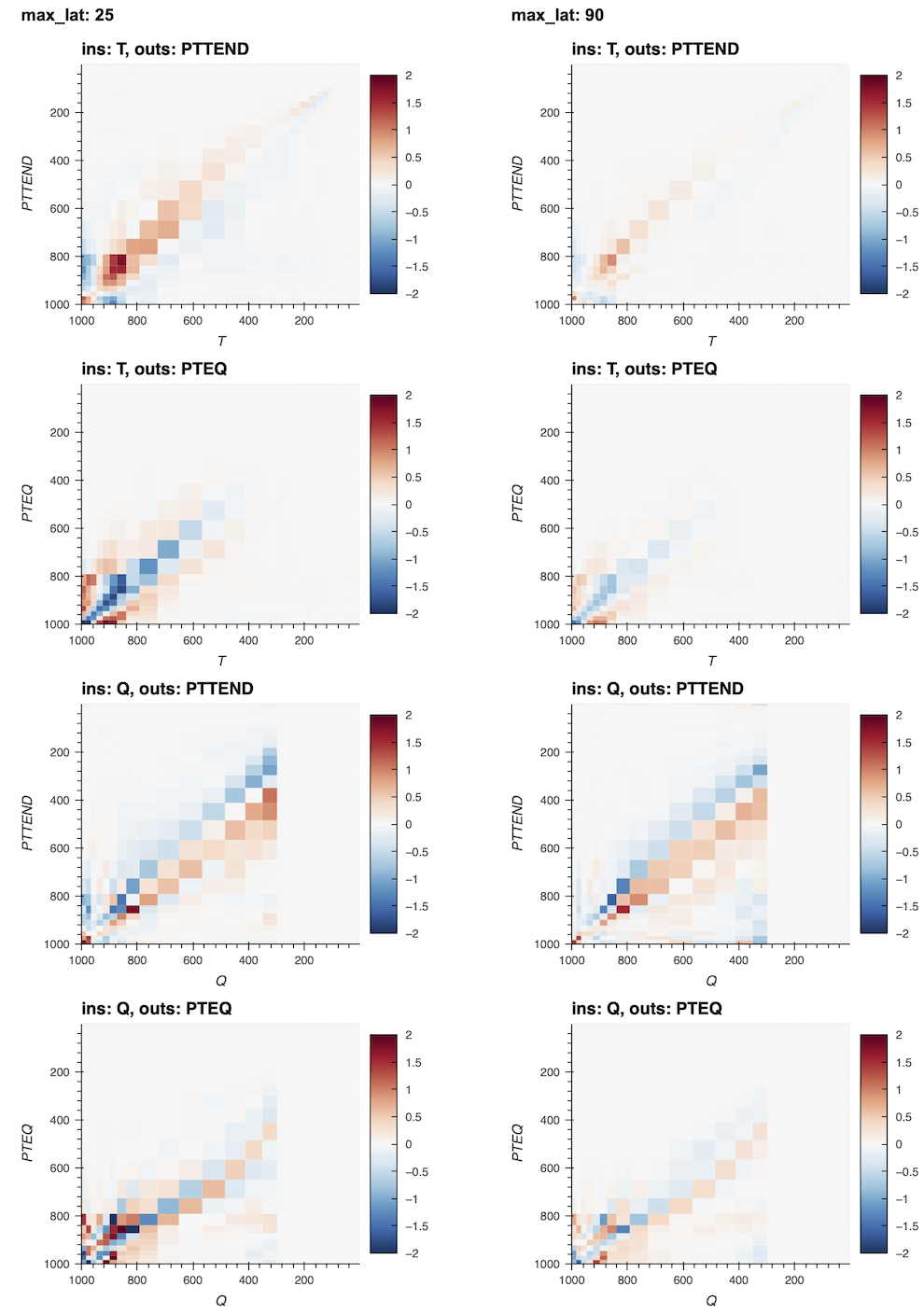Architecture Comparison

Jacobian CAM4 NN

Jacobian SPCAM NN

Bottleneck